摘要:规律探索类问题是广东省中考高频题型,探索解决此类问题的方法是非常有必要的。只依靠备考阶段的突击略显单薄,可以从对教材素材的价值深入挖掘,提炼出破解之法,将提高学生数学素养和解题能力落实到平时的教学中。
关键词:规律探索,压轴题,教材素材,破解
今年广东省中考试题第16题,考察了规律探索问题,本题作为填空题的压轴题,命题要求有一定的区分度,因此难度会有明显提升。而通过实际情况来看,学生得分的情况确实不是特别理想,对于规律探索类的题目,参加广东省考的学生和老师应该是很熟悉的,在2015年,2016年和2018年都出现过类似的题目,在备考中如何破解规律探索压轴题来谈一谈个人浅显的看法。
一、试题呈现
如图1所示的图形是一个轴对称图形,且每个角都是直角,长度如图所示,小明按图2所示方法玩拼图游戏,两两相扣,相互间不留空隙,那么小明用9个这样的图形(图1)拼出来的图形总长度是 (结果用含a、b代数式表示)
.png)
二、试题分析
规律探索问题是广东省中考的热门题型,近5年中考中,有4次出现此类问题,体现了命题的延续性。同时,这4次出现的题目,类型上又差异,2015年第15题是数字规律问题,2016年第21题是几何图形变化规律问题,2018年第16题是平面直角坐标系中的图形变化规律问题,2019年第16题是图形规律问题。这些变化也体现命题上的创新,对于同一类型的问题,从不同的命题方向切入。而2019年第16题,从基本图形到拼接方式,有别于传统的命题方式,有创新。这样的拼接方式,也更切近生活实际,体现数学的实用性。
本题虽然是填空题的压轴题,但是命题老师在编制此题时,还是表现出了对广大考生的关怀,将规律探索问题设置在有限个,而不是探索一般规律,适当的降低了难度。
三、解法展示
解法1:补全图形,直接计算。由于题目的图形已经画出了5个基本图形相扣,要破解9个图形拼出来的总长,只需要把剩下的4个图形画出来,得出完整的形状。通过观察图形,可以发现,总长度由5个a和4个间隔部分组成,而间隔部分的长度为,即可得出答案为。
本题要寻找9个基本图形拼出来的图形的总长度,9个基本图形的量不是非常大,而且题目图形已经给出了其中5个,对于思维能力和解题能力稍弱的学生,可以通过补全图形的方法来破解本题。此解法也体现了对考生情感态度的关注,面对困难题目,能够积极想办法解决。
解法2:观察图形的拼接方式,只有一个基本图形时,长度为a,加上第二个拼接时,增加的长度为b,此后再增加一个基本图形,增加的长度都是b,因此9个图形的拼接总长度为。
.png)
解法3:如果9个图形并排拼接,总长度为9a,按照两两相扣的方式拼接,则中间有8个重叠部分,每个重叠部分的长度为a-b,因此,实际总长度为9a-=
解法4:如图,在第一个基本图形和最后一个基本图形中,补上一个突出来的部分,总长度就变成了由10个a-b和9个2b-a组成,则总长为=
.png)
四、课本素材的启发
本题为图形规律探索问题,解法也非常丰富,但从学生的答题情况来看,得分情况并不是特别理想,说明学生对于此类问题的思路和解法掌握得不好。图形规律探索类问题,在教材中出现过,如果能把握好教材提供的素材,深挖它的作用,体现它的价值,对于这类问题的突破是非常有帮助的。
在初中数学北师大版七年级上册第三章第一节《用字母表示数》部分,提供了一个引入素材,虽然它的主要作用,是引出字母可以表示任何数,而且结论也已经通过教材的描述给出了。在教学中,不但要注重这个素材的结论,如果能更关注几个结论产生的过程,引导学生寻找不同解法的思路,不同解法的本质,提炼出解题的方法,就能轻松破解图形规律探索题。
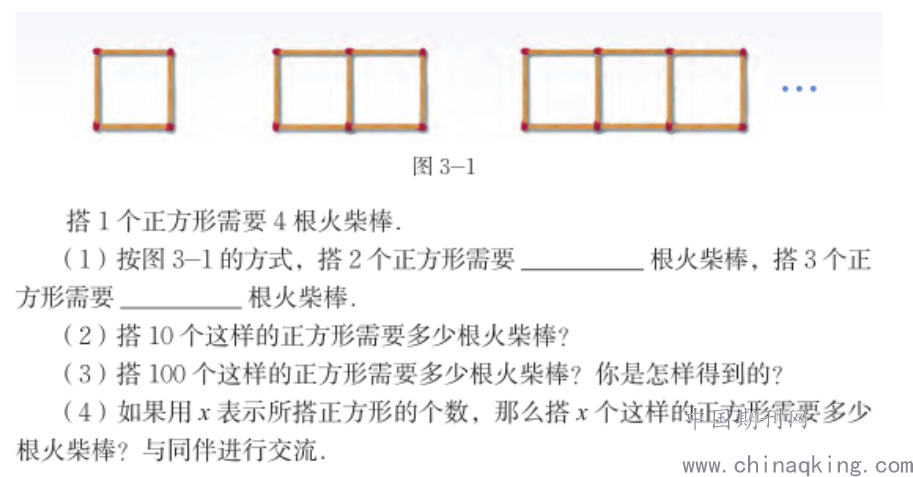
教材给出的第一种解法:“第一个正方形用4根火柴,每增加一个正方形增加3根火柴,那么搭x个正方形就需要火柴棒根”。有了结论再来对照题目,学生一看就能明白,但是这样能不能抓住问题的本质,进而迁移到其他类似问题呢?
对于这种教法,教学中要让学生搞清楚,4和3,以及x-1都分别代表什么,搞清楚每一个量的意义,才是完全理解和掌握了这种方法。4就是每一个基本图形的火柴数量,3是增加一个基本图形,原本是4根火柴,除开重叠部分的1根,实际增加三根。这个方法的关键是找出基本图形和重叠部分,进而找出每增加一个图形所增加的量。
对照第16题得解法2,我们可以发现,抓住了问题的本质,就轻松解决问题,基本图形长度为a,重叠部分为a-b,因此,增加的部分为,从而轻松得出结论。
教材给出的第二种解法为:“上面一排和下面一排都用了x根火柴,竖直方向用了(x+1)根火柴,共用了根火柴。”对照图形,此种解法也很容易理解,通过把整个图形拆分为三个部分,把每一部分都找出来,再合起来就是总数。教学中需要深入挖掘的是前面两个x的本质是什么,是拼接中每个基本图形的不变量,有多少个基本图形,上下就会分别有多少个不变量。
对照第16题解法4,通过对图形的处理,做一个拆分,把总图形分成两个部分,第一部分是每一个基本图形减去两边的重叠部分,找到每存在一个基本图形,就有一个中间部分,这部分长度为,再找到剩下的10个重叠部分,就可以破解问题。
教材的习题部分,给出了第三种解法:“小颖得出这样的结果:搭x个这样的正方形需要用根火柴棒,你认为她的结果对吗?你能说出她是怎么想的吗?”同样,要理解清楚此种解法的本质,总结出思路,提炼为方法。这种解法的思路是将x个基本图形排列,则总共有4x根火柴棒,两两之间重复一条边,则一共重复了根火柴棒,总数减掉重复的即可得出最后的结果。
第16题解法3,也是完全按照这种思路来解决问题的。先从整体上来看,找出没有重叠时的总长度,再找出每个重叠部分的长度为a-b,最后由总长减去重叠,即可破解此题。
五、备考感悟
中考备考工作初中数学教学最重要的阶段,但是备考这段时间相对于整个初中三年的内容,还是偏短,想要把所有的问题都在这个阶段解决,是比较困难的。因此,非常有必要在平时的教学中,引导学生透过问题解决,归纳解法,提升思维,总结方法和思想,解决中考热点问题。
教材的素材有非常重要的作用,中考命题很多时候也特别关注教材中的素材,在教学中要细致思考,深入挖掘这些素材的教学价值,充分发挥它们的作用,提升学生的解题能力和思维能力,形成方法,并能够迁移使用,达到以一题通一类的目的。
中考命题有延续性,很多热点题型出现的频率很高,但不会一味的照搬,在备考中要充分认识到这一点,对于同一题型或某一知识点,不能翻来覆去的练原题。要从不同的命题角度来备考,比如第16题,这种规律探索题近五年四考,但是每次命题的角度都是不同的。备考就要对规律探索类问题进行分类,然后再逐一突破。
规律探索题一般的解题策略是“特殊到一般再到特殊”,本次考试的这道图形规律题,寻找的是9个基本图形组合之后的总长度,我们可以直接从特殊入手,特殊结束,实际上就是降低了难度,只要学生补全图形,也是能够解决问题的。因此平时教学要鼓励学生面对难题,敢于积极动手,敢于迎难而上,就能够解决此类问题。