摘要:
数学思考作为数学课程总目标的一个重要方面,小学数学“综合与实践”的教学,是培养学生独立思考、学会思考的一个重要领域。如何深度挖掘和拓展“综合与实践”教材资源,提升学生的思辨能力?文章从挖掘真问-追问根源-探索规律-拓展资源等教学环节,激发思辨意识、体验思辨过程、促进思辨发展、提升思辨品质。
关键词:拓展 思辨
不学则殆。课堂上不乏遇到“此中有真意,欲辨已忘言”的现象。在小学数学教学中,“思辨”更多的是指数学思考、辨析能力。主要指“在观察、实验、猜想、证明、综合实践等活动中,发展合情推理和演绎推理,清晰地表达自己的想法。”
俞正强老师在《一个数学特级教师的思与行》中如是说“在教学实践中,我们的老师们基本上能够完成数学知识的学习,而没有数学思考的学习。如果没有数学思考的学习,数学学习就比较单薄。”如何进行深度拓展,使数学学习、数学思考厚重一些?下面以《数图形的学问》教学为例作以交流思考。
一、挖掘真问,激发思辨意识
要“数学地看待世界”,“数学教学活动应激发学生兴趣,调动学生积极性,引发学生的数学思考,鼓励学生的创造性思维。”这就要求教师应为学生创设真情境触及真问题,激发思辨意识。《数图形的学问》一课通过创设学生熟悉行车路线的问题情境,把生活中的现实问题抽象成数图形的数学问题。
片断一:课件出示
1.一辆汽车从石狮出发经过晋江到达泉州,你能画出示意图吗?
生画出示意图,展示交流:用点表示站点,用线段表示路线。用A、B、C分别表示石狮、晋江、泉州;用线段AB表示石狮到晋江……)
.png)
师:画得真好!我们通过画图,能把题目变得简明、形象。
2.师:关于车票,你可以提出什么数学问题?
生1:一共需要多少种车票?你们同意吗?你们还有意见吗?
生2:一共需要多少种车票?是问从石狮到泉州,还是石狮到泉州,泉州又返回石狮呢?
师:是啊,从石狮到泉州不返回,我们叫单程,从石狮到泉州又返回叫往返。只去不回,可以提问题:单程需要准备几种车票?
在这个教学片断中,教师舍去教材中的鼹鼠钻洞的情境,把难以理解的“任选一个洞口进入,向前走,再任选一个洞口钻出来”,创设为学生熟悉和行车路线问题情境,把生活中的现实素材抽象成数图形的数学资源,运用图形来描述和分析,使数学问题更简明、形象。充分理解用点表示站点,用线段表示路线。把“有多少条不同的路线?”改变为真情境里的真问题“单程需要准备几种车票?”引导学生联系生活实际,培养学生用数学的眼光看实际问题,用数学的思维思考实际问题,用数学的方式描述实际问题的能力。借用回答者的“你们同意吗?”“你们还有意见吗?”又询问倾听着的学生,激发学生的思辨意识。
二、追问根源,体验思辨过程
在数学学习中,要使学生思维活跃,如何教会学生分析问题的基本方法,这样就有利于培养学生的正确思维方式,使学生想得更清晰、更全面、更深、更合理。教学中,要体现数学本质特性,应当指导学生学会透过现象看本质,学会全面地思考问题,养成追根究底的习惯。
片断二:
1.出示图一:图中共有几条线段? (指名板演)
.png)
生3:我是这样数的,AB、BC、AC三条。
师:很好,只含有一段的线段是基本图形。比如线段AB、线段BC, AC是含有两段的线段,是组合图形,我们给起个名字叫 “二合一”线段。共有(2+1=3)段。
生3:你们同意吗?你们还有意见吗?
生4:我从A点出发,有AB、AC两条线段,从B点出发有BC一条线段,也有2+1=3条线段。你们同意吗?你们还有意见吗?(没有)
师:是的。两位同学画出两种画图方式,他们从多角度思考解决问题的策略。
2.请你数一数: 图中有几条线段?(出示图二) (温馨提示1.想办法不重复、不遗漏、有顺序地数。2.可以画一画,写一写,记录数的过程。)
.png)
(1)学生自主探索,指名上台讲解数的过程。
生5:我是这样数的,AB、BC、CD三条基本线段。(师记录下来)有AC、BD两条“二合一”线段,还有总的一条。一共有6条。你们同意吗?你们还有意见吗?
师:同学们给这条总的起个名字吧。(“三合一”线段)
生6:我从A点出发,有AB、AC、AD三条线段,从B点出发有BC、BD两条线段,从C点出发有CD一条线段,也有6条线段。你们同意吗?
师生互动:生5同学按段分类来数3+2+1的3表示(生:基本图形的个数),2表示(生:二合一图形的个数),1表示(生:三合一图形的个数)。这样数把每一类可能出现的情况都数出来了,体现同学们能够有序思考,不重复、不遗漏地数出线段总数。
生6按点的位置分类来数:先数完点A,共有(3条),再数点B ,共有(2条),最后数点C,有(1条),加起来也是6条。
师小结:像这样不重复、不遗漏、有顺序地数图形的过程,根据问题提供的信息,按一定的标准,从基本图形到组合图形、从短到长、从左往右把每类中可能出现的情况一一列举,数出线段的数量,这在数学上叫有序思考,是一种良好的数学学习品质。
.png)
只有经过细致缜密的思考,才能提高学生辨析的质量和价值。在这个片断教学中,教师创设民主、宽松、和谐的学习氛围,放手让学生进行观察、操作、猜测、辩论等活动,引导学生从不同的角度、不同侧面,多层次、多方位思考问题,从而得出多种数线段的方法。学生在获得知识的同时,充分感受学习数学的快乐,体验成功的喜悦,从根本上实现了由过去的“单向思维”向“多维思辨”的转变,学生真正成了学习的主人。
三、探索规律,促进思辨发展
对于规律的探索,渗透了数形结合、变中不变和从特例开始寻找规律等数学思想方法,提升探索、思辨、验证的数学学习能力,发展学生的数学核心素养。在教学中,学生根据初步经验,在观察比较、合作交流、推理归纳等数学活动过程,引导学生学会从特例开始寻找规律,探索规律,发现规律,运用规律。在学生不断深入的思考过程中,交流辨析中逐渐对自己的结论自我修正和进一步完善。思维在错误的修正中、在拓展的探究中、在你来我往的争执下、在跌宕起伏的辨析声中逐渐深刻起来。随着一个个问题的抛出,思维高潮的迭起,学生的发现由“井中之蛙”的感觉,慢慢发现一片“天”,随着表格的填充,渐渐发现更广阔的“天地”。整个过程学生都沉浸在探索的氛围中,促进思辨发展。
片断三:
1.出示问题:从石狮到福州有5个汽车站,单程需要准备几种车票?
师生交流得出:我们把现实问题抽象为简明的数线段的数学问题:共有几条线段?
2.填表。
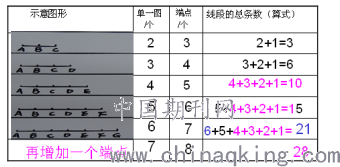
师:认真观察、分析表格,你发现了什么规律?
生1:我发现端点总是比基本图形数量多一个。你们同意吗?
生2:我有不同的意见。我发现有几个基本图形,线段总条数就从几倒着加到1。
生3:我还有一个发现。我发现有几个端点,线段总条数就从点数减1再一个一个倒加到1。你们还有意见吗?
生4:我发现每增加一个点,就增加了前面基本线段的条数。
生5:我发现基本图形的个数乘点数再除以2等于线段总数。比如:有6个基本图形,就用6×7÷2=21。
学生经历通过画图、观察、推理、列式等解决问题的过程,进行数学思考,发展探究与解决问题的能力,归纳与概括规律、探究解题策略的可行性和正确性。此时此刻,学生 “数学思维”不断碰撞与交融:专注的眼神,认同的点赞、会心的微笑、欣赏的点头;当不同的声音汇集而来,当学生的学习热情持续高涨,辩证在举例中生成、思维在辨析中提升。
四、拓展资源,提升思辨品质
综合与实践的综合不只是简单的拼凑和合并,小学数学课程的拓展也不是盲目的延伸和提高。综合与实践教学后期可向课后延续、向教学内容深度延续、向学生的思维格局延续。如何融合教学资源,拓宽学生的视野、丰富学生的数学经验,从而促进学生数学思维和能力的更好地发展?应该是“曲已终情未了”,只有提倡更有深度、更有宽度、更有广度的学习,增强数学教学的变化性,提供思维的广泛联想时间与空间,使学生在面对实际的综合的问题时,能够从多种角度进行思辨,真正成为“自己探路的人”,综合与实践教学的价值便得以体现。
片断四:
你还想研究什么图形?老师发现,同学们按着一定顺序来数的方法非常简单,这种方法是否也适用于数长方形和三角形呢?请你试一试。

学生完成交流汇报。
生1:我是这样数的,(1)中长方形中基本图形有2个,二合一的图形有1个,共有3个长方形。(2)也一样,长方形中基本图形有3个,倒着加,列式是3+2+1=6个,(3)长方形中基本图形有4个,列式是4+3+2+1=10个。
师:看来数线段的方法也适用于数长方形。
生2:数线段的方法也适用于数三角形,我是这样数的,三角形中的基本图形有4个,列式是4+3+2+1=10个。你们同意吗?你们还有意见吗?
生3:我有不同的数法:我是按边来数的,含有左边第一边的三角形有4个,第2条边往右边的三角形有3个,第3条边往右边的三角形有2个,第4条边往右边的三角形有1个,共有4+3+2+1=10个。
师:通过这几位同学的演示,看来数线段的方法也适用于数三角形。数三角形也可以按角来数、按边来数。学有余力的同学还可以研究下面的题目。
课外延伸:

课外延伸部分还可以研究数角、数梯形,以及①②③等多层图形,它属于三种不同的类型。其中①是上层三角形数+上下层三角形数即10+10=20个,或上层三角形数×层数10×2=20个。②是横列长方形数×竖列长方形数,即(3+2+1)×(2+1)=18个。③是平方数相加,即基本图形16个+四合一图形9个+九合一图形4个+十六合一图形1个=30个。
探索了这些数图形的学问,孩子们的研究还没有结束,他们在思考与辨析中进一步理清思路,明晰了认识。通过分析、比较、概括,孩子们又会发现,图形在变,方法没变,都是找基本图形、再找几合一的组合图形,以不变应万变。看,孩子们变中不变的数学思想又在综合与实践中得到提升。
从无序到有序,是一种思维的渐进过程;从自主探究到合作交流,是数学思维发展的上升过程;从自我建设,概括规律到与他人补充、修正,是一次次思维火花的碰撞;从课内到课外,是一次次思想的跳跃。《数图形的学问》只是小学数学综合与实践教学的冰山一角,要把传授数学知识与数学思想方法紧密结合,把训练学生思维与课堂教学紧密结合,要从深度挖掘教学资源、从广度拓展教学资源,多角度提高学生思辨能力,还需要我们一线教师不断努力、勤于研究。
参考文献
[1]中华人民共和国教育部.义务教育数学课程标准(2011年版)[M]北京:北京师范大学出版社,2012.
[2] 郑毓信.数学教育视角下的“核心素养” [J].数学教育学报,2016(3)
[3] 俞正强.种子课:一个数学特级教师的思与行[M].北京:教育科学出版社,2013.
作者简介:谢秀坤,福建省石狮市长福小学副校长。福建省农村小学骨干教师,泉州市骨干教师,石狮市教学名师。近年来十余篇论文泉州市及以上获奖。