岳娇娇
山东省威海市河北小学 264200
“深度数学”并不是“高难度数学”,而一定要用简易的手段,通过变易的方式,凸显数学的重难点,让学生能直观、直接观察到蕴含在数学问题中规律和感悟数学知识生成的过程,最终实现形成数学、使用数学、解释数学三个教学维度。下面我从四个“简”出发,阐述我的观点。
一、素材简练
【片断一】《公倍数和最小公倍数》
课前探究:用长3厘米,宽2厘米的小长方形能拼成边长是多少的正方形?
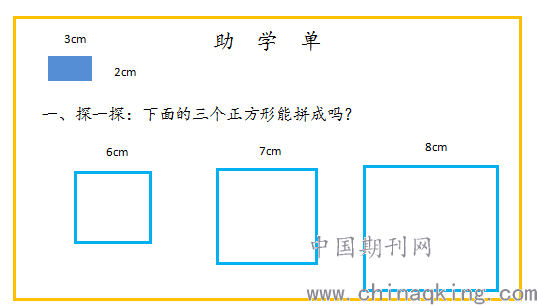
生1:可以拼成边长6厘米的正方形,7厘米和8厘米的不能拼。
师:还可以拼成边长是多少的正方形?你是怎样验证的?
生2:还可以拼成边长是12厘米的正方形(展示图片)
······
师:拼成的正方形的边长与小长方形的长和宽的关系是什么?
生3:我发现符合要求的正方形的边长既是3的倍数,又是2的倍数。
【评析】
离开了形象思维,抽象思维就像断了线的风筝。有了直观素材的支撑,才能促进学生观察、实验、猜测、验证及推理概括能力的发展。这节课的导入素材就是一个简单的拼图游戏,可谓简单至极。这样的教学从简单开始,“退”到学生思维的起点,在数形结合中发现规律,体验归纳推理的思考方法,真正想数学本质迈进。可见,教学素材的“丰富”与否,有时不是看我们呈现给学生多少不同的素材,而是看我们对素材的挖掘与把握的程度。
二、探究简要
【片断二】 《认识负数》
师:你能在温度计上表示出-3℃和+13℃吗?
(生探究)
生1:我们先找到0的位置,往上找到+13℃,往下找到-3℃。
师:只要先确定了0的位置,那么从0向下数就是零下的度数,
.png)
从0向上数就是零上的度数。
【评析】
这个环节“醉翁之意不在酒”,看似是简单地标注刻度,实则暗藏重难点。没有正负数的分界点,学生无处下笔,“逼迫”学生进一步思考——划分正负数的点是什么?这时,学生意识到0在认识正负数方面的重要性。“会学”“善学”比“学会”更重要。教师通过设计有思维含量的探究活动,让学生从思维定势中“跳出来”,反思提升。
三、学法简妙
【片断三】吴正宪 《搭配中的学问》
老师指着黑板上上衣和下衣连线
师:大家跟老师一起来数一数。唰!(配合动作:伸出3个手指,从上往下)1个3,唰!2个3。
师:如果再增加一件上衣,又有几种搭配?
生:唰!再增加1个3,共3个3,9种。
师:如果9件上衣,3件下衣,有几种搭配?
生:共9个3,27种。
【评析】
一件上衣同时搭三件下衣,让学生用“唰、唰”来读,读一个唰就是1个3,学生非常形象地体验到乘法原理。不是讲授,而是让学生自己体验。这样做,很有创意,学生的体验也就更深刻。简单的动作,巧妙地渗透了乘法原理。深度数学教学要让每一个孩子都能用适合自己的方式来学习,将有思想深度的数学内容变得容易一些。
四、练习简捷
【片断四】 顾志能 《分数乘除练习》
.png)
生1:最终结果是8
师:得数等于开始数,奥秘在哪里?
.png)
生2:过程中的三个分数,计算时变为, ,,约分后其实就是1,8乘1还是8。
师:若你也能编一道同类型题,才算是超级水平!
超级水平:
.png)
【评析】
教学应该是让学生思考在前,探究为先,教师的主要任务是引导而非简单讲解或机械灌输。在“数与代数”教学领域,教师不能“就题论题”,而要适当进行拓展,挖掘习题潜在功能。数学题目是做不完的,学生只有提高思维能力,才能后劲无穷。因此,我认为发展学生高阶思维是学生实现深度学习途径之一。
一节有内涵、有张力、有后劲的数学课堂,必定源自一位思想有高度、视野有广度、知识有长度、研究有厚度、思考有角度的数学教师。只有教师思考的不断“深入”,才能实现课堂教学有浓郁数学味的“简出”!