(浙江省永嘉县实验中学,325000)
摘要:山重水复疑无路,柳暗花明又一村。在初中数学的学习中经常出现这样的情境。本文主要探讨了初中数学教学中复杂问题的对策。把复杂问题数形结合整体化、简单化、图表化,可以有效地做到化繁为简,对培养学生的学习兴趣,提高他们解决实际问题的能力等方面有事半功倍的效果。
关键词:复杂问题;对策
兴趣是最好的老师。初中阶段的学生抽象思维逐渐形成,学生学习兴趣的培养显得格外重要。学生学习兴趣的培养和保持是每一个数学老师都必须高度重视的问题。数学教学中,难免出现一些较为复杂的内容,教师在教学中,必须想办法把这些问题化繁为简,变抽象为形象,才能提高学生的学习兴趣,让他们保持较高的学习效率,让学生在学中乐,在乐中学,达到最优化的课堂教学目标。
一、数形结合整体化
著名数学家华罗庚先生说:“数与形本是相倚依,怎能分作两边飞,数缺形时少直觉,形少数时难入微,数形结合百般好,隔离分家万事休。”这充分说明了数形结合思想在数学研究和数学应用中的重要性。如初一年级数学教学中的列车完全通过隧洞(或者桥梁)问题,物质的配送问题,其都可以通过画图形的方式,把各种复杂的等量关系直观化,形象化,取得最佳的教学效果。
如果只关注图形,忽视了数量关系,有时候学生处理找规律的题也会变得非常困难,因为他们往往把数和形机械地割裂开来,看形就是形,看数就是数。如按下列图形摆下去,第4个图形中有4个黑色六边形,请问第2018个图形中有多少白色的六边形?
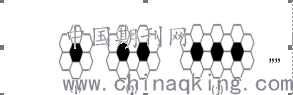
观察本题,我们可以得到以下数据:第一个图形有:6=4×1+2,第二个图形有:10=4×2+2,第三个图形有:14=4×3+2……通过这样的数据分析,学生很容易发现第n个图形的规律就是:4n+2。那么第2018个图形有:8084=4×2018+2。通过这样的数形结合,学生便能轻松解决这个问题,为他们数形结合思想的形成奠定一定的基础。所以教学中,把复杂的问题数形结合整体化,会取得事半功倍的效果,大家不妨一试!
二、复杂问题简单化
复杂问题简单化,指的是把复杂的问题看成一个整体,找到其中的本质规律从而加以简化。现实生活中的有些运动变化很复杂,但也有自己一定的规律,抓住了规律,其实也很简单。
如小明和妈妈在一条大街上散步,他们相向而行,街道长2千米,小明每小时走2千米,小明的妈妈每小时走3千米,小明同时牵着一条小狗,每小时走3千米,当狗碰到小明的妈妈时立即返回,当碰到小明又立即返回,如此反复,问小明和妈妈相遇时,小狗走了多少千米?表面看这是一个复杂的运动问题,如果把小狗走的路一段一段地割裂开来,的确有点复杂。可是我们可以简单一点来处理这个复杂的运动问题。从整体上来讲,只要知道小狗走的时间,就能知道小狗走的路程了。而小狗走时间,恰好是小明和妈妈相遇的时间,这样思考这个题目又变得格外的简单了。所以有时我们可以把一些复杂的问题分解成若干简单的问题,最后彻底解决它。
三、复杂问题表格化
电话已经成为每个家庭重要的通讯工具,关于电话的收费问题也成为每个家庭关注的问题。但对于仅有一元一次方程经验的初一学生的来说,怎样选择合适的方案还是有很大的难度。但只要我们合理的借助表格,学生就能轻松解决这个问题。例如:两种移动电话计费方式
.png)
观察完成后的表格,可以看出,主叫时间超出限定时间越长,计费越多,并且随着主叫时间的变化,按哪种方式的收费少也会变化。表格把数据进行分类整理,能够清楚地知道数据的增减变化,为方案的选择提供最直接的依据,具有较高的说服力,学生容易理解和接受。
总之,数学教学的目标,就是让学生轻松愉快地解决现实生活中的实际问题,解决问题的方法多种多样,数形结合整体化、简单化、图表化只是众多方法中一部分,我们教师应该引导学生找到解决问题的最优方法,给数学学习带来更多的乐趣。