沈阳市浑南区第五初级中学 孙萍 110000
摘 要:数学是一门非常严谨的学科,它具有严密的逻辑性和演绎性。随着我国教育形式的不断变革,现在的初中数学教学也在逐渐将新型教学技术应用到日常的教学工作中。几何画板作为一种新型的现代教学软件,是体现数形结合思想的重要工具,将其运用到初中数学教学中可以将图形之间的内在联系展现在学生面前,使抽象问题形象具体化,给学生更加直观的印象,从而加深学生对几何关系的理解,大大提高了课堂教学效率,取得更好的教学效果。而全等三角形是初中数学平面几何部分的重要知识,它既是前面所学图形的全等知识的延伸与拓展,又是后续学习探索三角形相似的条件的基础,并且是用以说明两线段相等以及两角相等的重要理论依据。本文我将结合探索三角形全等的条件为案例来阐述几何画板在优化初中数学教学中的应用。
关键词:几何画板、三角形全等、数形结合
一、几何画板在探索三角形全等的条件教学中的应用
全等三角形是两个三角形之间最简单、最常见的关系,在探索三角形全等的条件教学过程中,传统的数学教学中教师在进行这一部分的教学大多数采用的是板书+三角板+圆规或者PPT辅助的形式,教师独立完成画三角形,画完图形之后直接进行讲解,在这个过程中学生对图形的形成过程并不是很了解,而且由于是人工画图,画图的精准率很低,浪费大量时间。而在几何画板的应用下能够快速地将图形绘制好,绘图的精准率也得到了明显的提升,这对于初中的数学教学来说是很重要的,而将几何画板应用到探索三角形全等的条件的教学中可以更直观的让学生观察图形的形成及变化过程,同时可以保持在一些几何关系不变的前提下对图形进行拖拽和动画演示,加深学生对三角形全等条件的理解,及时突破教学重点和难点。
因此,本节课的知识在初中几何学习中具有承上启下的作用。经过自己的学习和不断探索,尝试使用几何画板软件进行本节内容的教学,收到了良好的教学效果。下面结合我自身的实际谈谈利用几何画板软件设计初中探索三角形全等的条件一课的几点做法。
1. 创设问题情境,使学生自主探究
数学是从问题开始的,每一节数学课都离不开问题,那么是教师一道一道的讲解呢?还是由学生自己去探究呢?我想这应该不是当代教师的问题,关键是问题情境的创设对学生是否具有一定的吸引力,一节好的数学课离不开教师的精心设计的每一个环节,当然一节课的引入创设情境也不例外。
在探索三角形全等的条件这一节课当中,学生在上一节课已经掌握了图形的全等的基础上,复习全等三角形的概念和全等三角形的性质并举例说明,接下来利用几何画板绘制三角形按钮先后绘制两个看起来大小一样的三角形,分别记为△ABC和△DEF(如图1),在前面已经掌握的知识的基础上试问学生△ABC和△DEF是否全等呢?你是如何验证你的想法的,这样很自然的导入了新课。
.png)
2.几何画板动态演示,验证猜想
根据生活经验,学生自然会想到用度量的方法,教师继续追问,我们应该怎么度量比较合适呢?只度量其中一个数据可以吗?两个呢?学生们很快就投入到思考与讨论中,你一言,我一语互相讨论起来,几分钟之后教师通过几何画板中的度量软件和拖动软件验证学生的猜想。
首先验证在△ABC和△DEF中有一个量相同是否能判定两个三角形全等,操作方法:使△ABC保持不变作为对照对三角形,在保证△DEF一条边的长度与△ABC一条边的长度完全一样的前提下,教师随意拖动△DEF其余边或者角,学生可以直观观察到△DEF与对照图形△ABC不全等(如图2)。
.png)
利用同样的拖拽方法验证在在一个角相等的前提下两个三角形是否全等,学生依然可以看到两个三角形不全等(如图3)。
.png)
其次验证△ABC和△DEF满足两个量一样是否能够判定这两个三角形一定全等,这里主要从以下三种情况着手进行研究:
情况一:保证两三角形两条边长度一样,通过几何画板变化△DEF两条边之间的夹角或者第三条边的长度,让学生观察变化的三角形△DEF与对照△ABC是否全等,学生通过数据的度量发现两个三角形不全等。之后会猜想如果△DEF两条边之间的夹角或者第三条边也和△ABC一样,这两个三角形可能会全等(如图4),此时要求学生记录猜想;
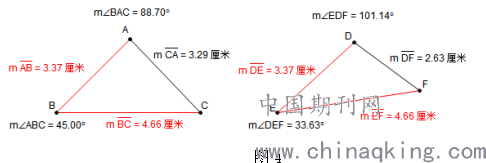
情况二:保证△ABC和△DEF其中两个角的大小一样,改变△DEF两个角之间的夹边的长度,让学生观察变化的三角形与不变的△ABC是否全等,学生仍然发现两个三角形不全等。进而自然会猜想到如果△DEF中∠EDF和∠DEF之间的夹边DE的长度和△ABC中∠BAC和∠ABC之间的夹边AB长度相等时两个三角形可能会全等,或者△DEF中EF或者DF的长度和△ABC中BC或AC的长度相等时两个三角形也可能会全等(如图5),此时要求学生记录猜想;;
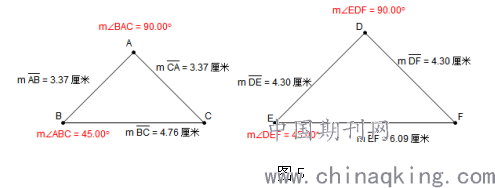
情况三:使△DEF中一条边的长度和一个角的大小和△ABC一样,改变△DEF其它边的长度或者角的大小,继续让学生观察变化的△DEF与不变的△ABC是否全等,学生仍然发现变化之后的△DEF和△ABC不全等,自然也会猜想出当△DEF的另外一个角也保持和△ABC中相对应的角大小相等时,两个三角形可能全等,此时仍然要求学生记录猜想;。
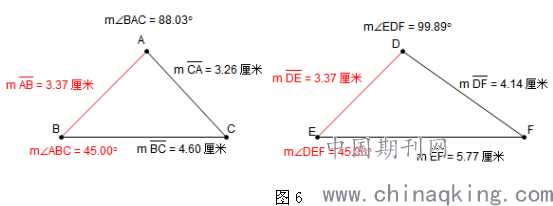
通过对以上以上试验,学生能够清晰看到,三种情况都不能判定△ABC和△DEF全等,进而学生自然会猜想到三个条件可以判定三角形全等,试验引发了学生进行了一些猜想,这时候教师仍然可以进行演示,对让学生提出的猜想进行验证,进而顺利得出三角形全等的结论?这样的操作直观易懂,激发了学生的探索求知欲和对数学学科的热爱,打破了传统枯燥无味的数学课堂,通过动态演示学生更加直观得出判断两个三角形全等需要三个条件。学生在这样一节课上经历了探索——猜想——证明这三个数学学习的必须阶段,使得知识成为条件化的知识,加深了印象并提高了学习数学的兴趣和课堂效率,轻松突破本节重难点。
以上是我在教学中应用几何画板进行探索三角形全等的条件的几点做法和想法,几何画板作为一种新的认知工具,其独特优势是任何传统的教学手段和模型所无法替代的,而且有良好的教学效果,在实践中,教师们通过自已的努力一定会创造出更加实用和更加符合学生认知规律的方案,为学生的学习更好地服务!
二、几何画板是体现数形结合思想的工具
众所周知,数形结合是一种很重要的数学思想,数学家华罗庚说过:“数缺形时少直觉,形缺数时难入微”。因此多数教师都非常重视数形结合思想的渗透与教学,上课时尽量地画好图形,力求使图形展现出其变化的趋势。但是,无论怎么画,怎么用一个又一个的幻灯片给学生展示,也只能给出一个“死图”,并不能体现图形的变化过程,而利用画板几何平台进行探索三角形全等的条件的教学,则可以绘制一幅幅有形有色会运动的“活”图,真正实现数形结合,增大数学课堂容量,通过变化让学生达到抛开现象看本质的效果。
参考文献:
[1]杜路敏.简析数形结合在函数和几何教学中的作用[J].学周刊,2013(19).
[2]徐丹丹.几何画板在初中平面几何教学中的应用研究[D].东北师范大学,2012.
[3]郭肖.基于几何画板培养学生动态解决几何问题能力的实践研究[D].东北师范大学,2012.