贵州省晴隆民族中学 封定红 贵州省晴隆县 561400
近年来,高考命题以立德树人,服务选才为导向,突显学科核心素养育人功能为根本任务。数学科则以注重对学生数学抽象、逻辑推理、数学运算、直观想象、数学建模、数据分析等六大核心素养能力考查为主线,以创新性为导向设置开放性试题(也称结构性条件不良试题)为代表,突出数学高考试题创新性原则,凸显数学文化功能、数学考试功能和学生实践创新能力考查。可以说,具备六大数学核心素养能力,是决胜高考数学的先决条件。
通过研究多年高考数学考题发现:“高考年年岁岁题相似,岁岁年年题不同”。这就要求教师在教学中采用探究式教学法,以学生为主导,摒弃实用主义和功利主义,以一题多解和一题多变为主线,合理数学文化知识有效进行分类,融入数学课堂教学之中,使课堂教学充满生机,内容丰富、丰满,为学生合理创造探究、讨论、质疑、充分自由表达的机会,多鼓励学生用自己的方法去探究和思考问题,让学生将自己所学的数学知识应用于解决实际问题,尝试用不同方法解决同一问题,使学生在“学知识——学表达——学知识”的过程初步体验数学发展、数学创造历程,最后引导对学生有效进行问题和问题解法归类、总结,形成结论,从而达到培养学生创造意识和创造能力的目的。
解析几何问题,是数学高考的重点和难点,是代数问题和几何问题相互转化,解答过程集数学运算能力、直观想象能力、数学建模能力、数据分析能力为一体,是历年高考常见试题,在总分值中占比大,多数年份以压轴题呈现,是“兵家”必争之地。下面给出我在解析几何教学中的几个案例。
案例一:巧用向量为工具,注重数形结合法体会一题多解或一题多变的教学手段,突破高考数学核心素养能力培养。
探究1:已知矩形ABCD中,AB=4, AD=2, E是BC的中点,求AE与DE夹角的余弦值。
.png)
探究1分析:(注重提问技巧,展示师生合作探究)
(1)师:提示学生,“同学们当你通过仔细审题后,你觉得这道题难吗?”
生:(这是一个较易解答的试题,可作如上的简图)
(2)师:如果这道题不难,那么你能用那些方法求解此题呢?请把你的思路与大家分享。
生1:(法一:使用勾股定理和余弦定理;
法二:使用勾股定理、添加辅助线、构造三角形、利用三角函数)
.png)
.png)
小结:此题利用数形结合法求解比较方便,所用的三种解法中,构建平面向量法最为简化,其余的两种方法作为平时训练有利于巩固三角函数的有关知识,它们各有优点。
案例二:问题中出现直线垂直,未出现向量或向量表达式,教学策略:注重数形结合、转化求解降难度,利用垂直得到向量数量积为零,从而突破难点,如2019年贵州省适应性考试理(文)科第20小题。
.png)
(1)(理科)当b>c时,A,B为椭圆C上的动点,且PA⊥PB,试问:直线AB是否恒过以顶点?若是,求出此定点坐标,若不是请说明理由。
(2)(文科)当c>b时,A,B为椭圆C上的动点,且PA⊥PB,试问:直线AB是否恒过以顶点?若是,求出此定点坐标,若不是请说明理由。
教学策略:
1、考点分析,考查的知识点:菱形面积,圆周长公式,求直角三角形斜边上的高,解方程组(估算检验法),向量的数量积,涉及到的方法:怎样解答直线是否恒过定点问题。
2、审题分析:此题第(1)问文理科都一样,若能作出简图,求解列式难度不大,但是要解方程组,方程组求解难度较大,导致很多学生到解方程组时就做不下去了,但是如果仔细审题第(2)小问中的(理科)当b>c时(或(文科)当c>b时)时就会发现第(1)问的b,c有2组值,可以使用连做带猜的方法解方程组,就能节省解方程组的时间,从而提高答题效率。
3、变式应用分析:第(2)小问理科与文科不同,文科的运算难度相对比理科小一些,教学时可将文科第(2)小问作为理科的变式训练;可将理科第(2)小问作为文科的变式训练,从而到达一题多变的训练要求。
.png)
.png)
.png)
.png)
.png)
.png)
.png)

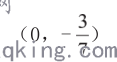
解答小结:
(1)过定点P(0,1)的直线分斜率不存在(特殊)和斜率存在(斜率为零时特殊),解答问题时可引导学生先特殊后一般的思考,通常特殊情况比一般情况更容易求解,本题中的第二问无论文科还是理科有一条直线斜率不存在另一条直线斜率为0都不成立,所以只考查一般情况就行。
(2)直线和圆锥曲线相交问题是很常见的数学考题,增分解答的一般步骤是:一,写直线方程(情况有多种);二,联立直线方程和圆锥曲线方程建方程组;三,将方程组消元,并设交点坐标,然后用韦达定理(根与系数)表达消元后方程中的有关量;四,再使用题中的已知条件列表达式求解即可。
(3)解答过程运算量大,要排除畏难情绪,要树立必胜信心、排除万难才能水到渠成。
总之,解析几何知识在高中高考命题时,以向量为基点的命题较多,教学时注重引导学生审明题意,数形结合,将向量构造、向数量积运算,垂直与向量数量积为0等只是相互转化,直线与直线垂直与直线斜率间关系相互转化,圆锥曲线定义的应用等知识一题多解或一题多变训练有效结合,就能突破高考命题中对“回归教材”解析几何知识考点,从而达到突出重点,突破考点,高效提高学生高考数学成绩的目的。